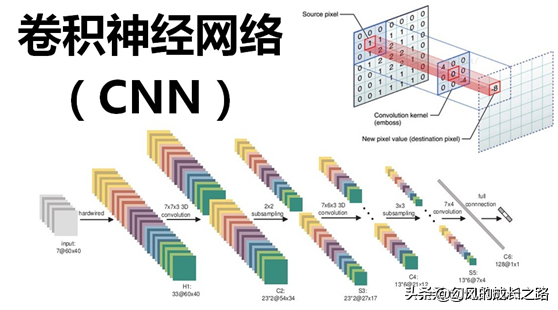
在深度学习领域，具有大力出奇迹的情况，一个模型只要足够大，数据足够多

在深度学习领域，具有大力出奇迹的情况，一个模型只要足够大，数据足够多，那么效果非常大的提升。

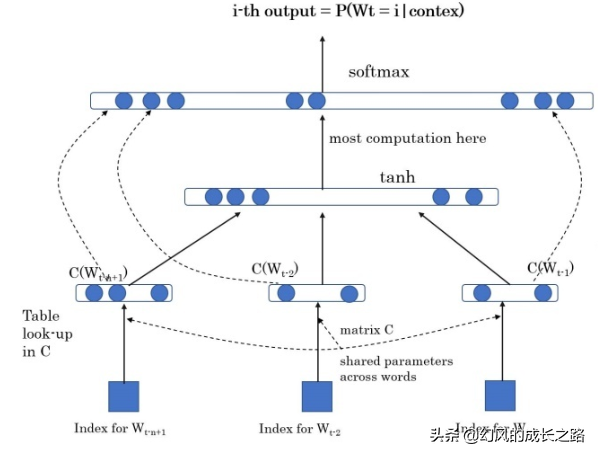
比如在自然语言理解领域，Bert横空出世，一下子开启了自然语言理解的预训练时代，只要数据足够多，计算力足够强大，Bert就能消化掉大量的数据，通过这种方式学习出来的动态词向量，你就是后面加上一到两层的全连接神经网络都比其它模型要强很多。

如果从数学角度来说，这里涉及到总体、个体、样本之间的关系。如果我们拥有这个任务的所有样本，也就是整体，那么就可以完整的学习到数据的分布情况，那么对于任何一个数据，我们都可以进行预测出准确的结果。

但问题是，我们无法获取到足够多的数据，我们只能获取到一部分数据，然后通过部分数据训练模型，然后进行预测。也就是说哪个模型能够通过已知数据来对数据整体的分布有一个强大的学习能力，那么这个模型的预测效果一定是更好的。

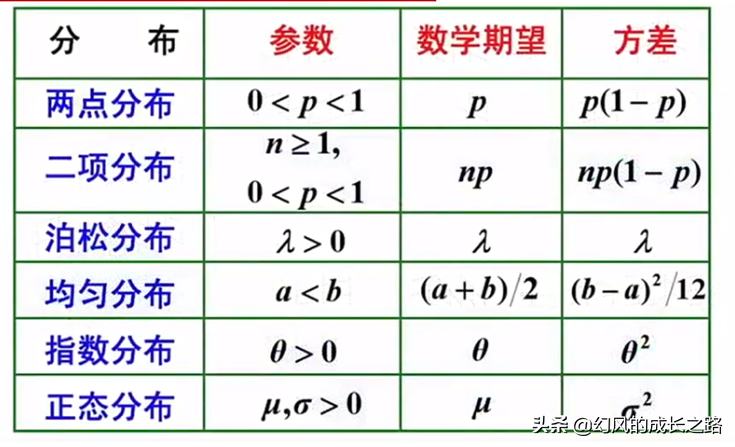
那么为什么数据越大越好呢？从数学极限定理和大数定律的角度可以知道，当随机变量的均值在随机变量的数量趋向于无穷时与其数学期望是无限接近的。中心极限定理也证实了，当数据量无限增加时，某些概率分布是以正态分布为极限分布的。

这两个极限定理都证明了一点，数据量越多，那么越能通过部分来表示整体，这就是大力出奇迹的概率基础。

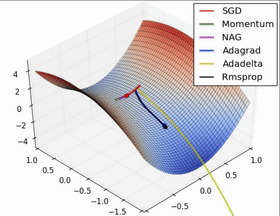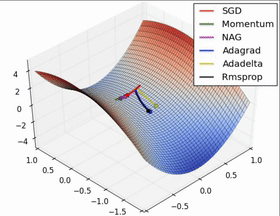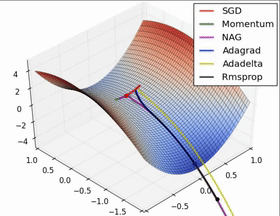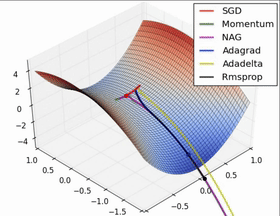
事实上，深度学习虽然是黑盒，这个黑盒其实并没有那么黑，它的黑只是它的优化过程，但其实它的理论是一值有支撑的，如果我们能够通过数学来支持深度学习的理论，那么数学就会变得非常的有意义，这也是我想要去做的。

《机器学习和深度学习之数学基础》目前正在打折优惠中，点击下方链接还可以领取优惠卷，并且免费阅读，欢迎订阅。